Simulation for Uncoded BPSK

• Link: video

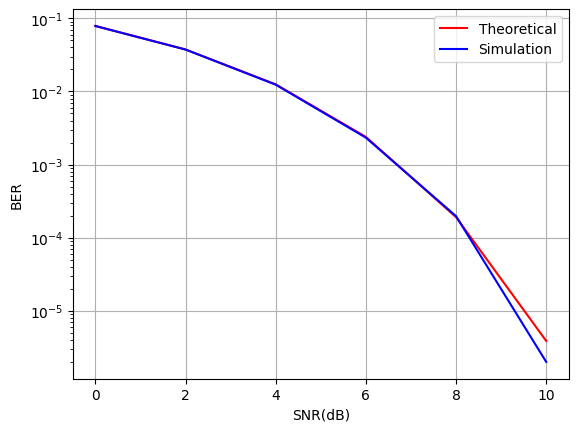
# Theoretical results $BER = Q(1/\sqrt{2SNR})$
import numpy as np
import math

SNRdB = 10
SNR = 10**(SNRdB/10)
R = 1 # rate of the code

BER_th = 0.5*math.erfc(math.sqrt(SNR))

# Implementing the simulation

N = 1000000
msg = np.random.randint(0,2,N)
s = 2*msg - 1
r = s + np.sqrt(1/2/R/SNR)*np.random.randn(N)

msg_cap = (r > 0).astype(int)

BER_sim = np.mean(msg != msg_cap)

print(f"BER theoretical = {BER_th}", f"BER simulation = {BER_sim}", sep='\n')

BER theoretical = 3.872108215522037e-06
BER simulation = 5e-06

## Graph
import matplotlib.pyplot as plt

plt.figure()

SNRs = np.arange(0, 12, 2)

BER_ths = []
BER_sims = []

for SNRdB in SNRs:
    SNR = 10**(SNRdB/10)
    BER_th = 0.5*math.erfc(math.sqrt(SNR))
    N = 1000000
    msg = np.random.randint(0,2,N)
    s = 2*msg - 1
    r = s + np.sqrt(1/2/R/SNR)*np.random.randn(N)
    msg_cap = (r > 0).astype(int)
    BER_sim = np.mean(msg != msg_cap)
    BER_ths.append(BER_th)
    BER_sims.append(BER_sim)
    
    # log scale
plt.plot(SNRs, BER_ths, 'r', label='Theoretical')
plt.plot(SNRs, BER_sims, 'b', label='Simulation')
plt.yscale('log')
plt.legend()
plt.xlabel('SNR(dB)')
plt.ylabel('BER')
plt.grid()

### 2.